
(再此先以直角三角型為例)
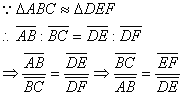

今天若將線段AB和角C的大小固定,改變角A的大小(前提為不破壞三角形),產生新的三角形AHI,其中角I等於角C,線段AB=線段AH
此時,再比較一次股和斜邊的關係:

,稱為角A的餘弦,用cosA代表,即cosA=
,稱為角A的餘切,用cotA代表,即cotA=
,稱為角A的正割,用secA代表,即secA=
![]()
![]()
![]()
![]()
![]()
![]()
2004 KSHS-218. All rights reserved.
| 三角函數 |  |
|||||||||||||||||||||||
| 三角函數的基本定義 | ||||||||||||||||||||||||
| 基本恆等式 | ||||||||||||||||||||||||
| 廣義角的三角函數 | ||||||||||||||||||||||||
| 由兩相似三角形的對應邊長會呈現一定比例關係的性質,我們發現一個特殊的性質: (再此先以直角三角型為例) |
||||||||||||||||||||||||
| 正弦定理 | ||||||||||||||||||||||||
| 三角形面積公式 | ||||||||||||||||||||||||
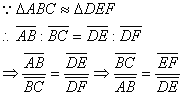 |
 |
|||||||||||||||||||||||
| 正弦定理的推導 | ||||||||||||||||||||||||
| 應用舉例 | ||||||||||||||||||||||||
| 餘弦定理 | ||||||||||||||||||||||||
| 餘弦定理的推導 | ||||||||||||||||||||||||
| 海龍公式 | ||||||||||||||||||||||||
| 兩相似三角形的股與斜邊之比值為一定值 今天若將線段AB和角C的大小固定,改變角A的大小(前提為不破壞三角形),產生新的三角形AHI,其中角I等於角C,線段AB=線段AH 此時,再比較一次股和斜邊的關係: |
||||||||||||||||||||||||
| 應用舉例 | ||||||||||||||||||||||||
| 正弦 餘弦兩定理的應用 | ||||||||||||||||||||||||
| 三角形面積 | ||||||||||||||||||||||||
| 在三角形ABC中,斜邊和股的比值為 |
|
 |
 |
|||||||||||||||||||||
| 四邊形面積 | ||||||||||||||||||||||||
| 中線長公式 | ||||||||||||||||||||||||
| 在三角形AHI中,斜邊和股的比值為 |
|
|||||||||||||||||||||||
| 三角形形狀 | ||||||||||||||||||||||||
| 例題 | ||||||||||||||||||||||||
| 我們發現,隨著角A的大小改變,斜邊與股的比值也會改變。 | ||||||||||||||||||||||||
| 參考資料 | ||||||||||||||||||||||||
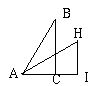
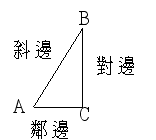
| 即 斜邊和股的比值為角A的函數,據此,我們將三角形所有的斜邊和股的比值列出來,並且一一給予名稱,但在此之前,我們得將兩個股分別命名,和角A相對的稱作對邊(線段BC),和角A相接的稱作鄰邊(線段AC): | ||||||||||||||||||||||||
|
|
,稱為角A的正弦,用sinA代表,即sinA= |
|
||||||||||||||||||||||
|
|
,稱為角A的餘弦,用cosA代表,即cosA= |
|
||||||||||||||||||||||
 |
||||||||||||||||||||||||
|
|
,稱為角A的正切,用tanA代表,即tanA= |
|
||||||||||||||||||||||
|
|
,稱為角A的餘切,用cotA代表,即cotA= |
|
||||||||||||||||||||||
|
|
,稱為角A的正割,用secA代表,即secA= |
|
||||||||||||||||||||||
|
|
,稱為角A的餘割,用cscA代表,即cscA= |
|
||||||||||||||||||||||
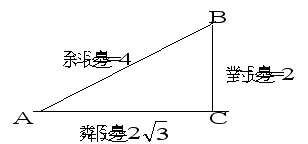
| 以角A為30度角,線段AC為2的直角三角型為例: | ||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
 |
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
| 到這裡,我們已經介紹完六種三角函數的基本性質囉! | ||||||||||||||||||||||||
| 2004 KSHS-218. All rights reserved. |
||||||||||||||||||||||||