當一個東西在轉動時，該如何描述他轉的角度呢？同樣說他轉120度，他可以轉順時針120度，當然，逆時針120度也行。那該如何用數學方式來描述呢？

一般來說，逆時鐘方向的角度取正值，而順時鐘方向的取負值。

現在將線段OA以O點為圓心逆時針旋轉一個150度，形成一個有向角，並且得到線段OA’則角AOA’即為150度。而我們將OA線段命名為始邊，OA’線段為終邊。如此一來，我們可以稱有向角O的大小為150度。

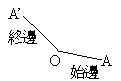
但是，如果OA’線段是由線段OA先旋轉360度，再旋轉150度，也就是總共轉510度而得到的呢？

這樣子，他的終邊依仍跟OA’一樣！所以有向角O也可能為510度。也因此，角度的大小就打破了180度的限制，而有更多更多的角度，這就稱為廣義角。

當然角度也能為負的，只要改為順時針方向就行！

然而，對這些始邊終邊相同而角度大小不同的有向角，我們叫他們為同界角。像390度、-390度、750度、-1110度，他們都是30度的同界角。也就是說
若角A和角B相差360度的整數倍，那他們就是同界角。

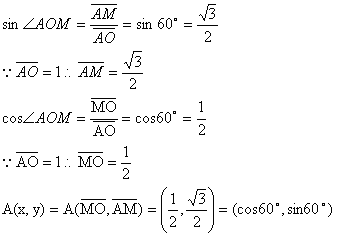
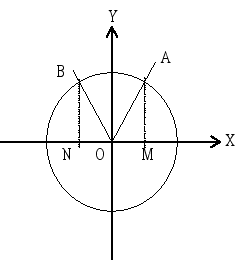
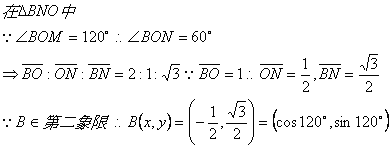
所以我們確定在單位圓上任一點，其座標可以用三角函數來表示是正確的。

而我們又從這兒推出另一個概念，在第二象限的角（簡稱第二象限角），他的sin值是正的，cos值是負的。（因為cos值為x座標的值，而第二象限之x值為負數）

再進一步推演之後，我們可以說：

第一象限角，sinA>0，cosA>0，tanA>0，cotA>0，secA>0，cscA>0
第二象限角，sinA>0，cosA<0，tanA<0，cotA<0，secA<0，cscA>0
第三象限角，sinA<0，cosA<0，tanA>0，cotA>0，secA<0，cscA<0
第四象限角，sinA<0，cosA>0，tanA<0，cotA<0，secA>0，cscA<0

現在，我們觀察一下右邊的圖形，可以發現一個現象！Ps.圖形中的圓半徑仍為1

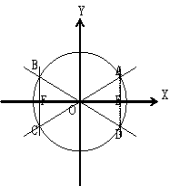
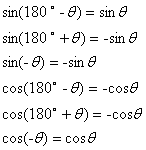
那關於之前的四種關係呢？他們都依仍成立

平方關係：

而倒數、商數兩關係，因為定義仍不變，故仍成立。

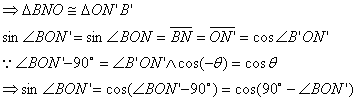
接下來，就朝著正弦定理出發吧！

連絡我們 | 雄中數學科 | 紅樓築夢 | ↑ top

2004 KSHS-218. All rights reserved.