
六個三角函數間,彼此也有一些互相的關係喔!
![]() 倒數關係
倒數關係
![]()
![]() 平方關係
平方關係
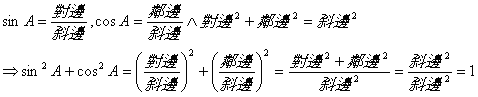
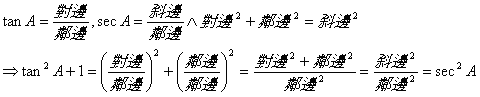
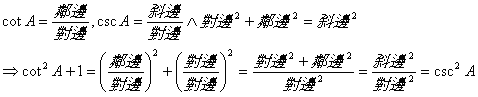
![]() 商數關係
商數關係
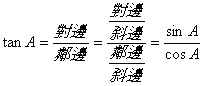
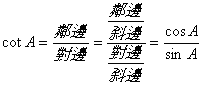
![]() 餘角關係
餘角關係
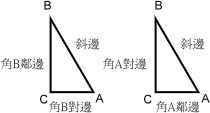
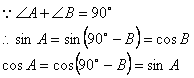
這個就稱作餘角關係,不只sin和cos有喔!tan和cot,sec和csc也有,簡單的說,若角A和角B互餘
(角A+角B=90度),則角A的正弦、正切、正割函數等於角B的餘弦、餘切、餘割函數。
![]() 關係六角形
關係六角形
由右邊的三角形,就可以表達上面的四種關係
倒數關係:
在對角線兩端的互為倒數。
平方關係:
若中間對角線代表1,則每個倒三角形中
上面兩個頂點平方的和為下面的點之平方
商數關係:
任選三個相鄰的頂點,兩旁頂點相乘等於中間的頂點
餘角關係:
高度一樣的兩個函數有餘角關係。

2004 KSHS-218. All rights reserved.